A deeper look at perceptual inference

In this post we will take a deeper look at how, according to the active inference theory, an organism assigns probabilities to its mental states about the world while observing it passively (without taking any action to change the world). This is called perceptual inference.

The simple example in the previous post showed how the human brain could according to AIF turn an observation into a probability over mental states representing what it observes using its generative model and Bayes’ theorem. Since there were only two interesting things in the garden scenario, a frog and a lizard, it was possible to calculate the posteriori probability distribution for the mental state as a closed-form expression (a “frog” with 73% probability). In real life there are too many possible mental states for the brain to be able to calculate the probabilities analytically.

This post describes how, according to active inference framework (AIF), an organism may get around the messy intractability of reality.

We don’t really know what’s out there

AIF posits that the generative model translates observations to probabilities for mental states, high-level representations of real-world states. The utility of mental states is probably to facilitate cognitive tasks such as storage of knowledge, decision making, communication, and planning, tasks that would be very hard on the abstraction level of observations only ¹.

A maybe trivial, but sometimes forgotten, fact is that a model is not the reality; the mental state is not the real-world state. An organism can only attempt to create, use, and store useful representations of the world in the form of mental states. These representations only capture certain aspects of the real-world states. Ontologically the model and the real world are two very different animals.

In case of frogs and lizards there is a straightforward correspondence between the mental state and the animal out there in the wild.

Some, perhaps all, mental states are also associated with an attribute that has not so far been observed in the real world, namely subjective experience. Examples of subjective experiences are green and pain [5]. We see not only a frog but a green frog. We not only see that our tooth is cracked and feel the crack with our tongue, we also feel the pain.

Mental states associated with subjective experiences are arguably useful as they are easy to remember, communicate, and act on. In some cases, like in case of severe pain, they are imperative to act on thereby giving a very strong motivation for the organism to stay alive (and, under the influence of other subjective experiences, procreate). I will return to this topic in a future post.

Some notation and ontology

We will in this post, like in the previous post, assume that all distributions are categorical, i.e., their supports are vectors of discrete events:

$$p(o) = \text{Cat}(o, \pmb{\omega)}$$

$$p(s) = \text{Cat}(s, \pmb{\sigma)}$$

Again, the above distributions mean for instance that $p(o_i) = P(O = o_i) = \omega_i$, i.e., $\pmb{\omega}$ is a vector of probabilities.

As stated before, the optimal way, according to AIF, for the organism to arrive at the probabilities for its mental states is by using Bayes’ theorem:

$$p(s \mid o) = \frac{p(o, s)}{p(o)} = \frac{p(o \mid s)p(s)}{p(o)} = \frac{p(o \mid s)p(s)}{\sum_s p(o \mid s)p(s)}$$

$p(o, s)$ is the brains generative model. It models how observations and mental states are related in general. It packs all information needed for perceptual inference.

$p(o, s) = p(o \mid s)p(s)$ where:

$p(s)$ is the organisms expectations about the probabilities of each possible mental state in the vector of all potential mental states $\pmb{S}$ prior to an observation.
$p(o \mid s)$, the likelihood, is the probability distribution of observations given a certain mental state $s$. This distribution can be seen as a model of the organism’s sensory apparatus.

The last piece of Bayes’ theorem is the evidence $p(o)$. It is simply the overall probability of a certain observation $o$. It would ideally need to be calculated using the law of total probability by summing up the contributions to $p(o)$ from all possible mental states in $\pmb{S}$:

$$p(o) = \sum_{s} p(o \mid s)p(s)$$

Since there is a large number of mental states, this sum would be very long making the evidence intractable.

Some intuition

The prior probabilities of mental states $p(s)$ is according to Bayes’ theorem modulated by the ratio $\frac{p(o \mid s)}{p(o)}$ to get the posterior probabilities of mental states. Let’s look at two examples to gain some intuition about this ratio.

Let’s say that we are looking at animals in a zoo and want to identify the species by doing an observation. We know that there are exactly ten animals, all of different species, in this small zoo and that the priori probability for seeing a certain species is the same for all ten animals (here identified with numbers from one to ten). $p(s)$ is therefore a uniform distribution that looks like this:

In the first case we assume that our observation is whether the sun is shining or not. We know that where we are, the sun shines $50\%$ of the time meaning that we get the following conditional probability in the nominator:

As stated above as an assumption, the evidense (denominator) is $p( \texttt{sunny}) = 0.5$. Therefore the ratio $\frac{p(\texttt{sunny} \mid s)}{p(\texttt{sunny})} = 1.0$ for all beliefs meaning that the posterior is equal to the prior; we have not learned anything from the observation which we of course new in forehand since knowing the weather doesn’t tell us very much about the animals in the zoo.

In the second case we are smarter and try to find a feature to observe that actually says something about the animal we are looking at. Let’s say that one of the animals is a dromedary and we observe a hump. Only the dromedary sports a hump so we are certain to observe hump for the $\texttt{dromedary}$ mental state and certain not to observe a hump for any other mental state. The nominator or the ratio now looks like this:

#4 is the $\texttt{dromedary}$ mental state.

The total probability of observing a hump is now $0.1$ since only one of the ten animals has a hump. The ratio $\frac{p(\texttt{hump} \mid s)}{p(\texttt{hump})} = 10$ for the $\texttt{dromedary}$ mental state ($s$). This means that if we observe a hump, the probability of a $\texttt{dromedary}$ mental state should increase by a factor of $10$. With the uniform prior probability distribution, the posterior probability for a $\texttt{dromedary}$ now becomes $10 \times 0.1 = 1.0$. We have gained enough information to now be certain that our mental state is $\texttt{dromedary}$.

How to calculate the intractable

There are ways to find approximations $q(s)$ to the optimal posterior distributions $p(s \mid o)$ without having to calculate $p(o)$:

$$q(s) \approx p(s \mid o) = \frac{p(o \mid s)p(s)}{p(o)}$$

Although $q(s)$ depends on $o$ indirectly, this dependency is usually omitted in AIF notation. $q(s)$ can be seen as just a probability distribution that is an approximation of another probability distribution that in turn depends on $o$.

One method to find the approximate probability distribution $q(s)$ is variational inference which can be formulated as an optimization problem. There is some empirical evidence suggesting that the brain actually does something similar [6].

$q(s)$ is usually assumed to belong to some tractable distribution like a multidimensional Gaussian. Variational inference finds the optimal parameters of the distribution, in this case the variance (vector) (or the covariance matrix) and the mean (vector). In the following the set of parameters is denoted $\theta$.

There are several optimization methods that can be used for finding the $\theta$ that minimizes the dissimilarity between $q(s \mid \theta)$ and $p(s \mid o)$. A popular one is gradient descent that is also used in machine learning. We assume that the inference of $q(s \mid \theta)$ is fast enough for $o$ and the generative model to remain constant during the inference.

Optimization minimizes a loss function $\mathcal L(o, \theta)$. The Kullback-Leibler divergence ² $D_{KL}$ measures the dissimilarity between two probability distributions and is thus a good loss function candidate for active inference:

$$\mathcal L(o, \theta) = D_{KL}\left[q(s \mid \theta) \mid \mid p(s \mid o) \right] := \sum_{s} \log\left(\frac{q(s \mid \theta) }{p(s \mid o)}\right) q(s \mid \theta)$$.

$\mathcal L(o, \theta)$ equals zero when both distributions are identical (all logaritms equal zero). It can be shown that $\mathcal L(o, \theta) \gt 0$ for all other combinations of distributions.

The loss function unpacked

Let’s try to unpack $\mathcal L(\theta, o)$ into something that is useful for gradient descent:

$$\mathcal L(o, \theta) = D_{KL}\left[q(s \mid \theta) \mid \mid p(s \mid o) \right] = \sum_{s} \log\left(\frac{q(s \mid \theta) }{p(s \mid o)}\right) q(s \mid \theta)=$$

$$\sum_s \log\left(\frac{q(s \mid \theta)p(o) }{p(o \mid s)p(s)}\right) q(s \mid \theta)=$$

$$\sum_s q(s \mid \theta) \log q(s \mid \theta) – \sum_s q(s \mid \theta) \log p(o \mid s) -$$

$$\sum_s q(s \mid \theta) \log p(s) + \sum_s q(s \mid \theta) \log p(o) =$$

$$\sum_s q(s \mid \theta) \log q(s \mid \theta) – \sum_s q(s \mid \theta) \log p(o \mid s) -$$

$$\sum_s q(s \mid \theta) \log p(s) + \log p(o)=$$

$$\mathcal{F}(o, \theta) + \log p(o)$$

With:

$$\mathcal{F}(o, \theta) = \sum_s q(s \mid \theta) \log q(s \mid \theta) -$$

$$\sum_s q(s \mid \theta) \log p(o \mid s) – \sum_s q(s \mid \theta) \log p(s)$$

$\mathcal{F}(o, \theta)$ is called variational free energy or just free energy ³. Since $\log p(o) $ doesn’t depend on $\theta$, $D_{KL}\left[q(s \mid \theta) \mid \mid p(s \mid o) \right]$ is minimized when $\mathcal{F}(o, \theta)$ is minimized meaning that we can replace our earlier loss function with free energy.

$\mathcal{F}(o, \theta)$ can be made differentiable with respect to $\theta$ which means that it can be minimized using gradient descent. An estimate of the loss function in each iteration can be found using Monte Carlo integration which means that we only take a few samples from $q(s \mid \theta)$, not the full distribution, do the multiplications and the summation. We then calculate the gradient of this sum with respect to $\theta$ and adjust $\theta$ with a small fraction (the learning rate) of the negative gradient [1]. Note that $p(s)$ and $p(o \mid s)$ are assumed to be quantities available to the organism for use in the calculation of the loss function.

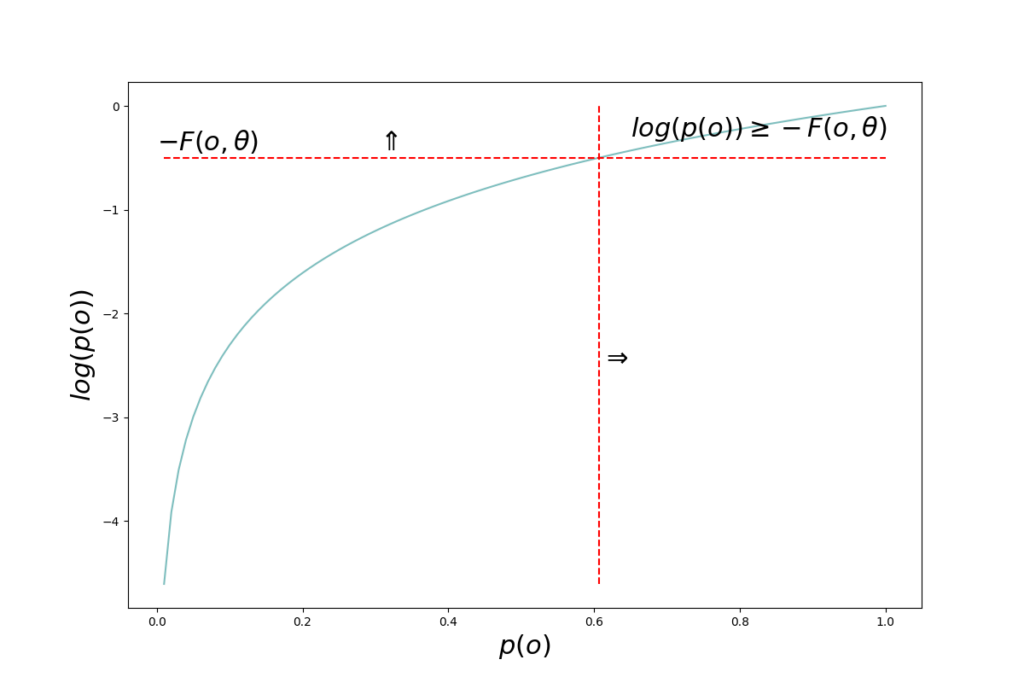
The quantity $– \mathcal{F}(o, \theta)$ is in Bayesian variational methods denoted evidence lower bound, ELBO, since $D_{KL}\left[q(s \mid \theta) \mid \mid p(s \mid o)\right] \geq 0$ and therefore $\log p(o) \geq – \mathcal{F}(o, \theta)$.

Note that the quantity $– \log p(o) $ remains unchanged during perceptual inference. The observation is what it is as long as the actor doesn’t change something in its environment that would cause the observation to change as a consequence.

$-F(o, \pmb \theta)$ is the lower bound for $log p(o)$. This means that as $F(o, \pmb \theta)$ is minimized (goes toward zero), $p(o)$ is “pushed” toward unity.

Surprise

The quantity $– \log p(o)$ can be seen as the “residual” of the variational inference process. It is the part that can not be optimized away, regardless of how accurate a variational distribution $q(s \mid \theta)$ we manage to come up with. $p(o)$ is the probability of the observation. If the observation has a high probability, it was “expected” by the model. Low probability observations are unexpected. $– \log p(o) $ is therefore also called surprise. High probability $p(o)$ means low surprise and vice versa.

From above we have $\log p(o) \geq – \mathcal{F}(o, \theta) \Rightarrow -\log p(o) \leq \mathcal{F}(o, \theta)$ meaning that the free energy is an upper bound on surprise; surprise is always lower than or equal to free energy.

According to AIF, the organism strives to minimize surprise at all times as surprise means that the organism is outside its comfort zone, its expected or wanted mental states. To minimize surprise, the organism needs to take action to make the observation less surprising. Minimizing surprise will be the topic of coming posts.

Links

[1] Khan Academy. Gradient descent.
[2] Volodymyr Kuleshov, Stefano Ermon. Variational inference. Class notes from Stanford course CS288.
[3] Thomas Parr, Giovanni Pezzulo, Karl J. Friston. Active Inference.
[4] Hohwy, J., Friston, K. J., & Stephan, K. E. (2013). The free-energy principle: A unified brain theory? Trends in Cognitive Sciences, 17(10), 417-425.
[5] Anil Seth. Being You.
[6] Andre M. Bastos, W. Martin Usrey, Rick A. Adams, George R. Mangun, Pascal Fries, Karl J. Friston,
Canonical Microcircuits for Predictive Coding, Neuron, Volume 76, Issue 4, 2012, Pages 695-711.

The distinction between observations and mental states may not be so clear cut but a matter of degree. A pure observation, like the sight of a linear structure, is void of semantics whereas the mental state representating a whole object such as a face, has a lot of semantic content. There are several layers of representation between the pure observation and the final mental state with increasing degree of semantics. ↩︎
Technically $D_{KL}$ is a functional which is a function of one or more other functions. $D_{KL}$ is a function of $q(s, \pmb \theta)$. The square brackets around the argument are meant to indicate a functional. Intuitively one can think of a functional as a function of a large (up to infinite) number of parameters, namely all the values of the functions that are its arguments. ↩︎
The term is borrowed from thermodynamics where similar equations arise. Knowing about thermodynamics is not important for understanding AIF though. $\mathcal{F}(o, \theta)$ is sometimes written as a functional like this: $\mathcal{F}[q; o]$. This is a more general expression as it doesn’t make any assumptions about the probability distribution $q$. ↩︎